Dr Andrzej Görlich

Sonata grant

Project description

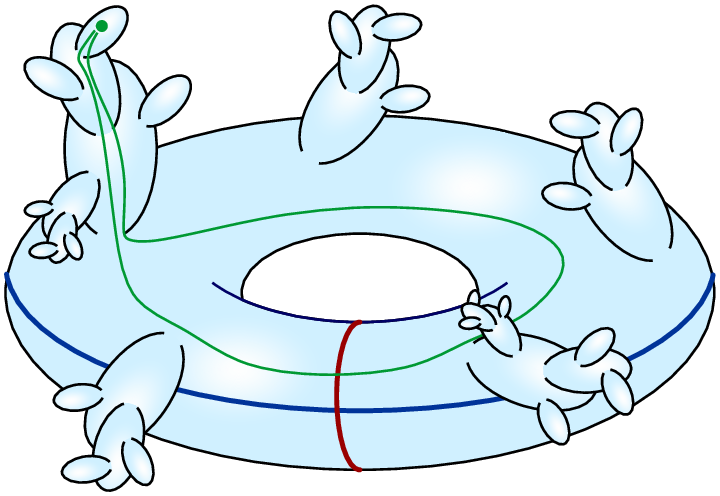The aim of the project is to analyze interactions between matter and quantum geometry of spacetime within the model of Causal Dynamical Triangulations (CDT) in four dimensions. One of the major challenges facing theoretical physics is to create a quantum theory of gravity. The method of Causal Dynamical Triangulations is a relatively new model proposed by Jan Ambjørn, Renate Loll and Jerzy Jurkiewicz, precisely with the aim of reconciling the classical theory of gravity with quantum mechanics. The CDT model is a nonperturbative and lattice formulation of quantum gravity from first principles, path-integral formalism, lattice regularization and general relativity. The already obtained results are very promising, the model predicted emergence of a semi-classical background geometry consistent with Einstein's equations with superimposed quantum fluctuations of the spatial volume, described by the minisuperspace model by Hartle and Hawking. The project consists in introducing to the model massive point particles, in the form of the trajectory located on a dynamic spacetime geometry, and massive scalar fields. The purpose of the project is to study the impact of such defined matter on the quantum geometry. Although there is no interaction term for the particles in the action, the particles are a source of the gravitational field and their trajectories should be effectively coupled through the quantum geometry of spacetime. Of particular importance would be the observation of the classical gravitational force in the quantum model and determination of quantum effects. In order to have an interesting, realistic quantum cosmological model, one has to add matter. Such result would be very riveting because the primary requirement on a quantum theory of gravity is its correspondence with general relativity. A key element in lattice field theory is to define a continuum limit. Usually it is associated with the existence of a secondorder phase transition. The first studies on the renormalization group flow of bare coupling constants have been already conducted by the author of the project in order to achieve the continuum limit. The consequence of adding a scalar field is to appoint a phase diagram and determine which points can be associated with theory's ultraviolet border. The project addresses also the problem of understanding the geometrical structure of three-dimensional spatial slices and describing their time evolution. The CDT model imposes a global proper-time foliation of spacetime, but its leaves do not have a physical meaning. Thick slices, which reveal different behavior, will be constructed. It is planned to analyze time propagation of fluctuations of the spatial geometry.

The research will employ methods developed in the frameworks of general relativity, quantum field theory, lattice field theory, renormalization group and computer science. The basic research tools in four-dimensional model of Causal Dynamical Triangulations are numerical computer simulations. The CDT model provides a regularization of a formal gravitational path-integral by introducing a discretization of the spacetime geometry via four-dimensional simplicial manifolds. At each stage Wick rotation to imaginary time is allowed, and then return to real time. In the imaginary time the quantum histories are weighted by a real factor that can be interpreted as a probability of a trajectory (space-time geometry). Such form allows the use of Monte Carlo simulation methods. The continuum limit will be studied by the methods of scale analysis, very similar to that used in the vicinity of phase transitions in statistical physics.

The project focuses on novel and yet not solved issues concerning the theory of quantum gravity. It addresses the problem, of coupling matter fields to four-dimensional Causal Dynamical Triangulations, of analyzing propagation of layers of constant time and of developing new methods of studying phase transitions in models with dynamical background. Analytical tools for describing the coupling of matter fields and quantum geometry will be created as well as numerical software within CDT model with matter, involving massless and mass scalar field, and one or two mass lines. Realization of the project involves publishing results in prestigious scientific journals and presentations at international conferences. The project will be conducted in international cooperation with Jan Ambjörn (Niels Bohr Institute, Denmark) and Renate Loll (Radboud University Nijmegen, The Netherlands and Perimeter Institute, Canada).

Main project themes

• Inclusion of massive point particles into the CDT model
• Study of the impact of a mass line on quantum geometry
• Study of interaction between two particles
• Study of interaction of a particle and a scalar field
• Analysis of time propagation of quantum spatial geometry fluctuations
• Development of new methods for the analysis of phase transitions

Publications

Towards an UV fixed point in CDT gravity

J. Ambjørn, J. Gizbert-Studnicki, A. Görlich, J. Jurkiewicz, D. Németh
Journal of High Energy Physics 07 (2019) 166

Causal Dynamical Triangulations is an attempt to formulate a non-perturbative lattice theory of quantum gravity. We describe the phase diagram and analyse the phase transition between phase B and phase C (which is the analogue of the de Sitter phase observed for the spherical spatial topology). This transition is accessible to ordinary Monte Carlo simulations when the topology of space is toroidal. We find that the transition is most likely first order, but with unusual properties. The end points of the transition line are candidates for second order phase transition points where an UV continuum limit might exist.

Critical phenomena in Causal Dynamical Triangulations

J. Ambjørn, D. Coumbe, J. Gizbert-Studnicki, A. Görlich, J. Jurkiewicz
Classical and Quantum Gravity (2019)

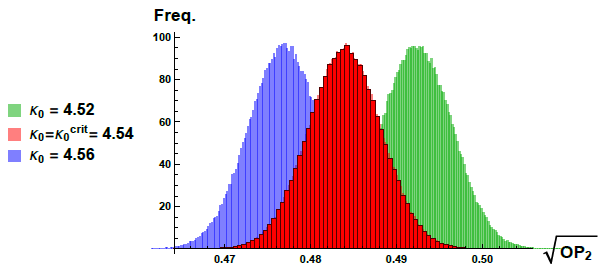Since Causal Dynamical Triangulations is a lattice theory of geometries, the phase transitions, which in usual lattice field theories are used to define the continuum limit of the lattice theory, will be transitions between different types of geometries. This picture is interwoven with the topology of space which is kept fixed in the lattice theory, the reason being that “classical” geometries around which the quantum fluctuations take place depend crucially on the imposed topology. Thus it is possible that the topology of space can influence the phase transitions and the corresponding critical phenomena used to extract continuum physics. In this article we perform a systematic comparison between a CDT phase transition where space has spherical topology and the “same” transition where space has toroidal topology. The “classical” geometries around which the systems fluctuate are very different it the two cases, but we find that the order of phase transition is not affected by this.

Pseudo-Cartesian coordinates in a model of Causal Dynamical Triangulations

J. Ambjørn, Z. Drogosz, J. Gizbert-Studnicki, A. Görlich, J. Jurkiewicz
Nuclear Physics B 943 (2019) 114626

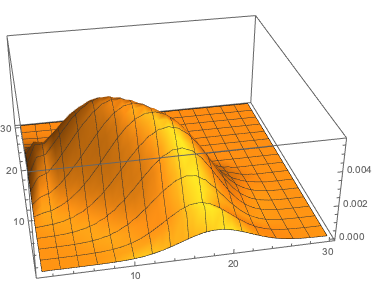Causal Dynamical Triangulations is a non-perturbative quantum gravity model, defined with a lattice cut-off. The model can be viewed as defined with a proper time but with no reference to any three-dimensional spatial background geometry. It has four phases, depending on the parameters (the coupling constants) of the model. The particularly interesting behavior is observed in the so-called de Sitter phase, where the spatial three-volume distribution as a function of proper time has a semi-classical behavior which can be obtained from an effective mini-superspace action. In the case of the three-sphere spatial topology, it has been difficult to extend the effective semi-classical description in terms of proper time and spatial three-volume to include genuine spatial coordinates, partially because of the background independence inherent in the model. However, if the spatial topology is that of a three-torus, it is possible to define a number of new observables that might serve as spatial coordinates as well as new observables related to the winding numbers of the three-dimensional torus. The present paper outlines how to define the observables, and how they can be used in numerical simulations of the model.

The phase structure of causal dynamical triangulations with toroidal spatial topology

J. Ambjørn, J.Gizbert-Studnicki, A. Görlich, J.Jurkiewicz, D. Nemeth
J. High Energ. Phys. 06 (2018) 111

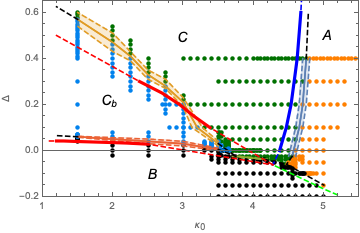We investigate the impact of topology on the phase structure of fourdimensional Causal Dynamical Triangulations (CDT). Using numerical Monte Carlo simulations we study CDT with toroidal spatial topology. We confirm existence of all four distinct phases of quantum geometry earlier observed in CDT with spherical spatial topology. We plot the toroidal CDT phase diagram and find that it looks very similar to the case of the spherical spatial topology.

Four-dimensional CDT with toroidal topology

J. Ambjørn, J. Gizbert-Studnicki, A. Görlich, K. Grosvenor, J. Jurkiewicz
Nucl. Phys. B 922 (2017) 226

Four-dimensional Causal Dynamical Triangulations describe a quantum theory of fluctuating geometries without the introduction of a background geometry. If the topology of space is constrained to be that of a three-dimensional torus we show that the system will fluctuate around a dynamically formed background geometry which can be understood from a simple minisuperspace action which contains both a classical part and a quantum part. We determine this action by integrating out degrees of freedom in the full model, as well as by transfer matrix methods.

New higher-order transition in causal dynamical triangulations

J. Ambjørn, D. Coumbe, J. Gizbert-Studnicki, A. Görlich, J. Jurkiewicz
Phys. Rev. D 95 (2017) 124029

We reinvestigate the recently discovered bifurcation phase transition in causal dynamical triangulations and provide further evidence that it is a higher-order transition. We also investigate the impact of introducing matter in the form of massless scalar fields to causal dynamical triangulations. We discuss the impact of scalar fields on the measured spatial volumes and fluctuation profiles in addition to analyzing how the scalar fields influence the position of the bifurcation transition.

Causal Dynamical Triangulations with Toroidal Topology

A. Görlich
Acta Phys. Pol. B 10 (2017) 311

Causal Dynamical Triangulations (CDT) is a background-independent approach to quantum gravity which provides a lattice regularization. In the case of spherical spatial topology, a universe with geometry of a four-sphere emerges dynamically in the so-called de Sitter phase. Imposing toroidal spatial topology changes this picture significantly and the average spatial volume profile becomes constant. Although no background geometry is put in by hand, the full quantum theory of CDT is able to identify a classical background geometry with superimposed quantum fluctuations. We determine the effective action for spatial volume by measuring the covariance matrix and show how to heal the problem of uniform volume profile.

Characteristics of the new phase in CDT

J. Ambjørn, J. Gizbert-Studnicki, A. Görlich, J. Jurkiewicz, N. Klitgaard, R. Loll
Eur. Phys. J. C 77 (2017) 152

The approach of Causal Dynamical Triangulations (CDT), a candidate theory of nonperturbative quantum gravity in 4D, turns out to have a rich phase structure. We investigate the recently discovered bifurcation phase C_b and relate some of its characteristics to the presence of singular vertices of very high order. The transition lines separating this phase from the “time-collapsed” B-phase and the de Sitter phase C_dS are of great interest when searching for physical scaling limits. The work presented here sheds light on the mechanisms behind these transitions. First, we study how the B - C_b transition signal depends on the volume fixing implemented in the simulations, and find results compatible with the previously determined second-order character of the transition. The transition persists in a transfer matrix formulation, where the system’s time extension is taken to be minimal. Second, we relate the new C_b - C_dS transition to the appearance of singular vertices, which leads to a direct physical interpretation in terms of a breaking of the homogeneity and isotropy observed in the de Sitter phase when crossing from C_dS to the bifurcation phase C_b.

Distribution of periodic trajectories of C-K systems MIXMAX pseudorandom number generator

A. Görlich, M. Kalomenopoulos, K. Savvidy, Savvidy G.
Int. J. Mod. Phys. C 28 (2017) 1750032

We are considering the hyperbolic C-K systems of Anosov–Kolmogorov which are defined on high dimensional tori and are used to generate pseudorandom numbers for Monte-Carlo simulations. All trajectories of the C-K systems are exponentially unstable and pseudorandom numbers are represented in terms of coordinates of very long chaotic trajectories. The C-K systems on a torus have countable set of everywhere dense periodic trajectories and their distribution play a crucial role in coding and implementation of the pseudorandom number generator. The asymptotic distribution of chaotic trajectories of C-K systems with periods less than a given number is well known in mathematical literature, but a deviation from its asymptotic behavior is unknown. Using analytical and computer calculations, we are studying a distribution function of periodic trajectories and their deviation from asymptotic behavior. The corresponding MIXMAX generator has the best combination of speed, size of the state and is currently available generator.

Impact of topology in causal dynamical triangulations quantum gravity

J. Ambjørn, Z. Drogosz, J. Gizbert-Studnicki, A. Görlich, J. Jurkiewicz, D. Nemeth
Phys. Rev. D 94 (2016) 044010

We investigate the impact of spatial topology in 3+1-dimensional causal dynamical triangulations (CDT) by performing numerical simulations with toroidal spatial topology instead of the previously used spherical topology. In the case of spherical spatial topology, we observed in the so-called phase C an average spatial volume distribution n(t) which after a suitable time redefinition could be identified as the spatial volume distribution of the four-sphere. Imposing toroidal spatial topology, we find that the average spatial volume distribution n(t) is constant. By measuring the covariance matrix of spatial volume fluctuations, we determine the form of the effective action. The difference compared to the spherical case is that the effective potential has changed such that it allows a constant average n(t). This is what we observe and this is what one would expect from a minisuperspace GR action, where only the scale factor is kept as dynamical variable. Although no background geometry is put in by hand, the full quantum theory of CDT is also with toroidal spatial toplogy able to identify a classical background geometry around which there are well-defined quantum fluctuations.

Funding

This research is funded by the National Science Centre, Poland, through the project SONATA 9 number 2015/17/D/ST2/03479.